林俊鈺／國研院高速網路與計算中心副研究員，協助推廣產學界的高速計算應用，研究興趣為平行計算與天文物理。

游輝樟／成功大學物理系副教授，專長為數值相對論與計算天文物理。

 

就在廣義相對論（General Relativity, 1915）及重力波的預測（1916）之後的百年，重力波物理儼然進入另一個階段：在美國的兩座雷射干涉儀重力波天文台（LIGO）於 2015 年 9 月首次觀測到雙黑洞碰撞事件；以及 2017 年 8 月，歐洲 Virgo 重力波天文台加入觀測網當月，首次觀測到雙中子星碰撞事件。未來偵測到重力波事件的頻率將愈來愈高，並且伴隨著電磁波段、微中子的觀測，將提供天文學更多資訊，開啟以重力波資訊解讀宇宙的新領域。

目前，公里等級的地面重力波干涉儀，被設計來偵測重力波造成的干涉臂微小長度變化。高靈敏度是它的強項，卻也是最大的罩門，會受到各種來自如地震、熱擾動、光壓、量子起伏……等的干擾，造成反射鏡的震動與干涉臂長度變化。因此科學家應用各種精密工藝，測量真正的重力波效應。座落在地表的干涉儀，號稱與太空站一般地平靜穩定。即使如此，未處理過的重力波訊號還是深埋在各種已知或未知雜訊中。因此，若能夠事先知道重力波波形，就能較容易地以所謂的「模板匹配」技術，從原始訊號中辨識出來。

 

精解愛因斯坦方程式

這需要精確地求解愛因斯坦方程式，了解不同重力波波源所造成的微小時空彎曲，也就是描述時空局部長度「度規」的變化，並計算相應的干涉臂長度改變時間序列。雙黑洞碰撞，也是主要的重力波來源之一。雖然單一黑洞是相當單純的球對稱物體，在廣義相對論發表的次年就有的精確解：史瓦西黑洞。但擴展到雙黑洞，並計算它們從旋進互繞（inspiral）、碰撞融合（plunge and merge）到鈴震（ringdown）並逐漸靜默成單一黑洞三階段的完整波形，卻也花費了近百年，直到 2005 年才有第一個整段的數值波形。除了因為碰撞瞬間難以用理論解析求解外，愛因斯坦方程式的非線性特徵，也讓初始的雙黑洞重力場並非簡單地個別黑洞疊加。除非相距足夠遠，牛頓重力足以合理地近似，但這又會讓後續的數值模擬花費太久時間在互繞旋進階段，這就是數值相對論所遇到的兩難。

長時間的模擬有其觀測上需求。因為，模板匹配其實就是做「已知波形與不同時刻觀測的乘積」的積分（即所謂的卷積），得出最大的相關性。因此模板波形週期愈多，得到的信噪比愈高。

數值上的第一個難題來自於廣義相對論是四維協變的理論，亦即不同四維座標選取都會給出相同的方程式，看不太出「時間演化」的概念。單單將廣義相對論表示成三維空間動力學方程式的想法，即所謂的 3+1 空間與時間分解，就花了近半世紀。最後由阿諾威特（Richard Arnowitt ）、戴瑟（Stanley Deser）及米斯納（Charles Misner）三位在 1962 年實現，表達成「ADM 公式」。

數學上，它與愛因斯坦方程式完全等價，只是又特地將時間的維度挑出來，還原成物理學家所熟悉「受拘束初值問題」。如此一來，理論上只要指定了合理、滿足拘束條件的初始三維空間與物質（能量）分佈，剩下的就交給大自然（廣義相對論）決定了。

利用 ADM 公式， 第一個軸對稱、等質量的雙黑洞迎頭對撞模擬，就在 1964 由 IBM 的哈恩（S. Hahn）及紐約艾德菲大學的林德奎斯特（R. Lindquist）所發表。並在接下來十多年間，一再改進，主要由德州大學奧斯汀分校的德威特（Bryce DeWitt）與他的學生斯馬爾（Larry Smarr）等人所進行。不過，這時對初始雙黑洞時空還不清楚，因此這些早期工作是使用相當簡化的 Misner 蟲洞模型，以類似「把手」、聯結空間兩點的蟲洞模型，作為模擬初始資料。這些模擬很快就不穩定發散了，無法繼續觀察融合後的黑洞細節，但估計對撞損失了約 0.1% 的總質量，變成重力波輻射，遠遠小於後來以圓軌道旋進的雙黑洞碰撞所釋放的能量。

不難想像這個先驅工作的困難度。當時連「黑洞」一詞都還沒出現，那要到 1967 年才被惠勒（John Wheeler）正式提出；一些關於黑洞的理論，如霍金與潘洛斯（Roger Penrose）的奇異點理論──證明在相當一般的條件下，夠重的星體塌縮就會形成奇異點與黑洞──也才剛萌芽。另一方面，在 60 年代末期，IBM 的通用型主機才逐漸開始普及，計算力僅約 1 MFLOPS，合 10⁶ FLOPS（floating-point operations per second ，每秒雙精度浮點運算次數，且記憶體僅有 1 MB）的數量級。在近期能買到的 Intel i7 桌上型 CPU，其計算力約為數十個 GFLOPS 數量級。

 

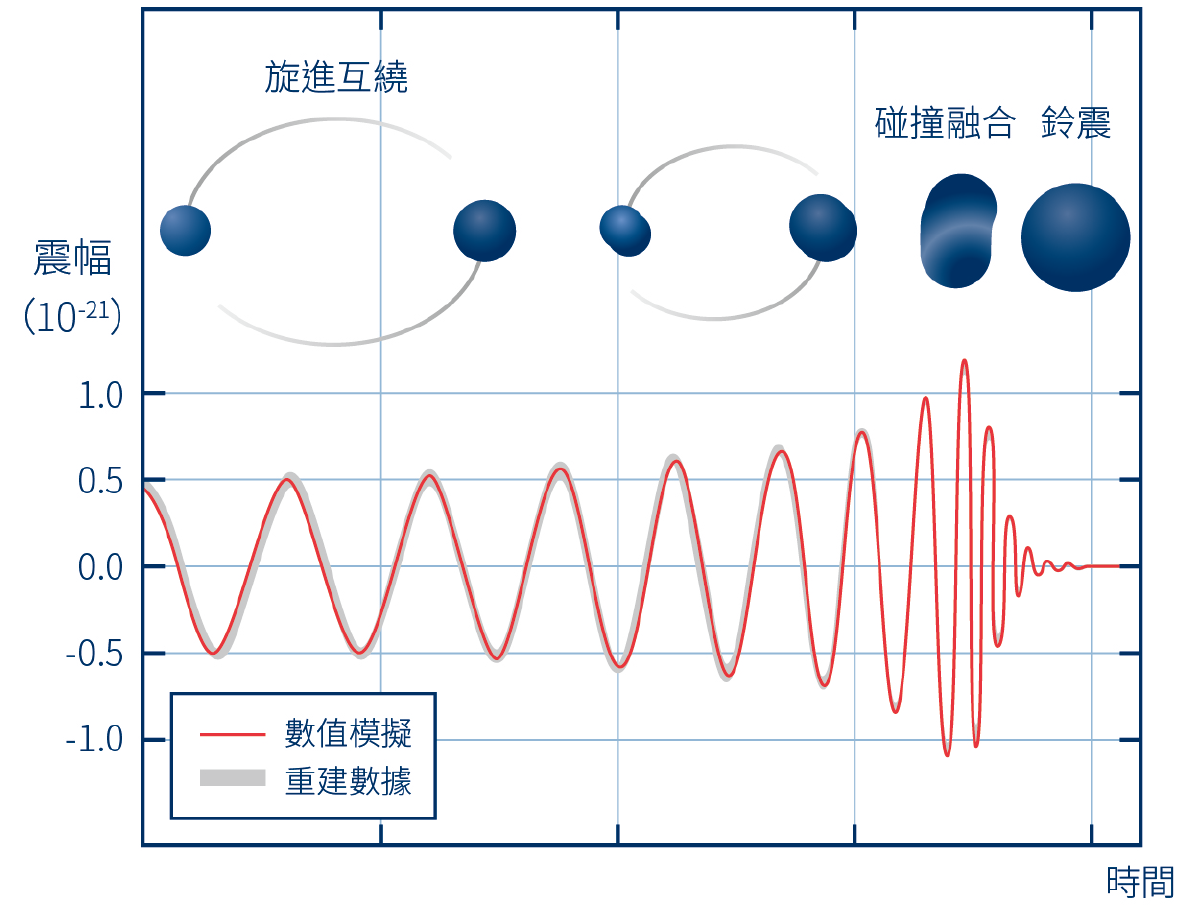
▲圖一：旋進互繞、碰撞融合到鈴震三階段的黑洞融合波形，縱軸為震幅，橫軸為時間，紅線（或灰線）為首次重力波事件 GW150914 的數值模擬結果，分別對應雙黑洞逐漸靠近的互繞、碰撞、並靜默成單一黑洞的過程。

 

黑洞研究計畫層出

1993 年的「雙黑洞碰撞與重力波挑戰計畫（Binary Black Hole Grand Challenge Project）」驅動了另一波黑洞模擬的進展。這是當年美國的「挑戰計畫：高速計算與通訊（Grand Challenges: High Performance Computing and Communication）」其中的一個提案。塞德爾（Edward Seidel）、斯馬爾與現在身兼聯科集團創辦人孫緯武教授等人作了一系列工作，包括計算更高階的重力輻射、以及與黑洞相當接近時的解析結果（close limit）比較。雖然仍是軸對稱的模擬，但已經可以觀察到黑洞融合後事件視界合併的演化。他們的工作也是 1995 年《Science》期刊的封面故事：其中的綠色管狀圖形顯示雙黑洞融合的過程，朝上為時間方向，黃線是剛好緊臨事件視界的臨界類光曲線，標示著黑洞的邊界。

這個「挑戰計畫」的科學目標是計算黑洞碰撞波形，但所帶來的附加價值是累積這種複雜非線性方程式的模擬演算法與經驗，作為大型平行計算設施的領航應用之一。與之同時，全球也開始舉辦一年兩次的 TOP500 超級電腦評比，延續至今，每年分別在美國及歐洲的超級電腦大會上公佈。當時，最快的超級電腦計算力約為 100 GFLOPS（=10¹¹ FLOPS），並且效能持續以每年約 1.8 倍的速度成長至今^註一。目前全球第一的超級電腦是中國無錫超算中心的「神威太湖之光」，計算力達 100 PFLOPS（=10¹⁷FLOPS）數量級（2017 年 11 月）。^註二

第一個全 3+1 維黑洞模擬在 1995 年完成了。幾乎同一組人馬，以笛卡兒座標下的 ADM 公式完成單黑洞的模擬，雖僅持續了 50 M，這卻也是好幾個黑洞的時間尺度了^註三。他們使用了 inking Machines CM-5、Cray C90 等超級電腦。同時代在德國馬普研究所的布魯曼（B. Brugmann）團隊開始使用了網格細化，以「越接近黑洞奇異點越細、解析度越高」的不均勻網格來減少不必要的計算量。這時，第一個版本的開源數值相對論程式套件（Cactus）也釋出了，基於早期在國家超級電腦應用中心（National Center for Supercomputing Applications, NCSA）的數值相對論研究，後來部分成員轉到波茨坦的馬普重力研究所、或稱愛因斯坦中心，開發數值相對論所需的共通程式，以減少重複發明輪子、重複開發類似程式碼的必要。如今，各研究群可在它的程式架構下貢獻自己的模組。當然，若想在計算方法上有所突破，還是免不了自行開發全新的程式，這也是目前許多數值相對論研究群在嘗試的。在 1997 年，布魯曼以所謂的「穿刺法」描述初始黑洞，使黑洞可帶有任意自旋與速度形成互繞系統，實現第一個雙黑洞融合瞬間的三維模擬，人們開始得以一窺融合瞬間的重力波波形。

在 21 世紀前的黑洞模擬都只穩定維持不到 100 M 數量級時間。我們現在理解這並非因為黑洞奇異點、或不好的數值方法，而是 ADM 方程式本身的演化就不穩定：只要初始資料有一丁點偏離了廣義相對論的約束方程，這偏差就會指數地增加，並不適合數值計算。雖然，數學上，只要初始資料完全滿足約束方程，不穩定就不會發生，但在有限位數的電腦上計算就會出問題。

在還沒穩定的長時間模擬結果前，人們在 2000 年後提出 Lazarus 計劃，嘗試結合後牛頓進似、數值計算與維擾方式，來介接前段旋進、短暫的中段模擬碰撞、與後段鈴震的雙黑洞融合波形。他們借用聖經中 Lazarus 死而復活的故事，來隱喻理論波形可描述旋進階段、在融合階段失效、然後又可以微擾理論計算後段鈴震波型（復活）。科學家創意展現於此：在受限的理論、技術、與資源下，作最恰當的近似討論，推進知識的邊界。

 

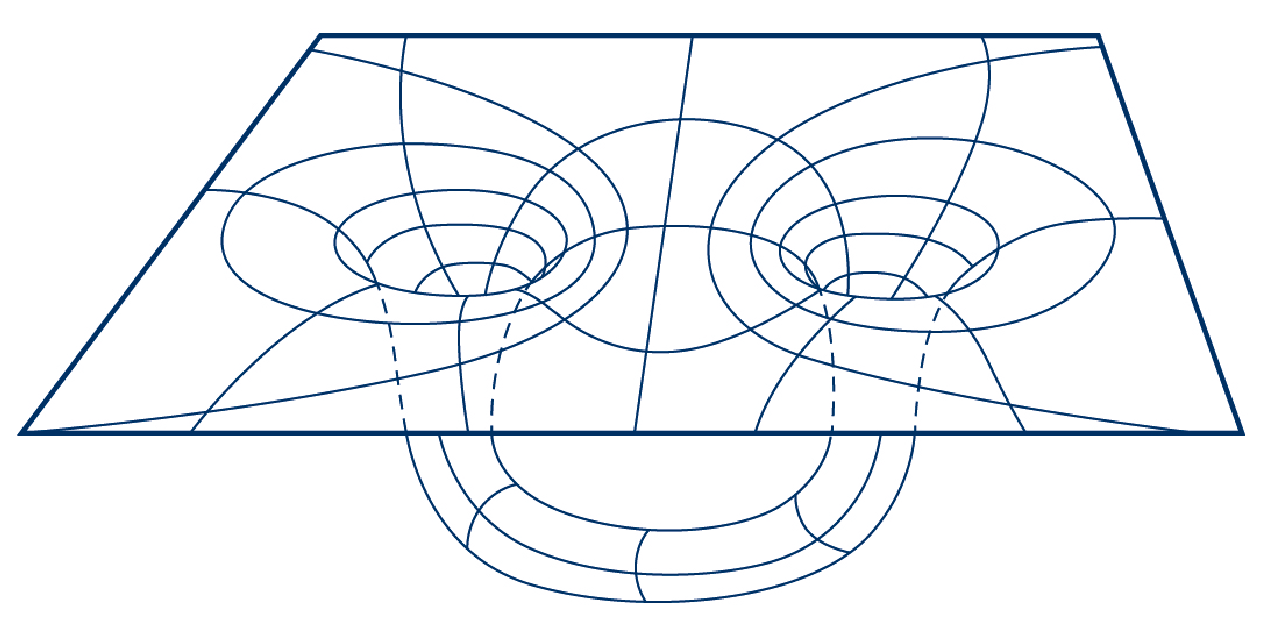
▲圖二：連結空間的兩點的 Misner 蟲洞。

 

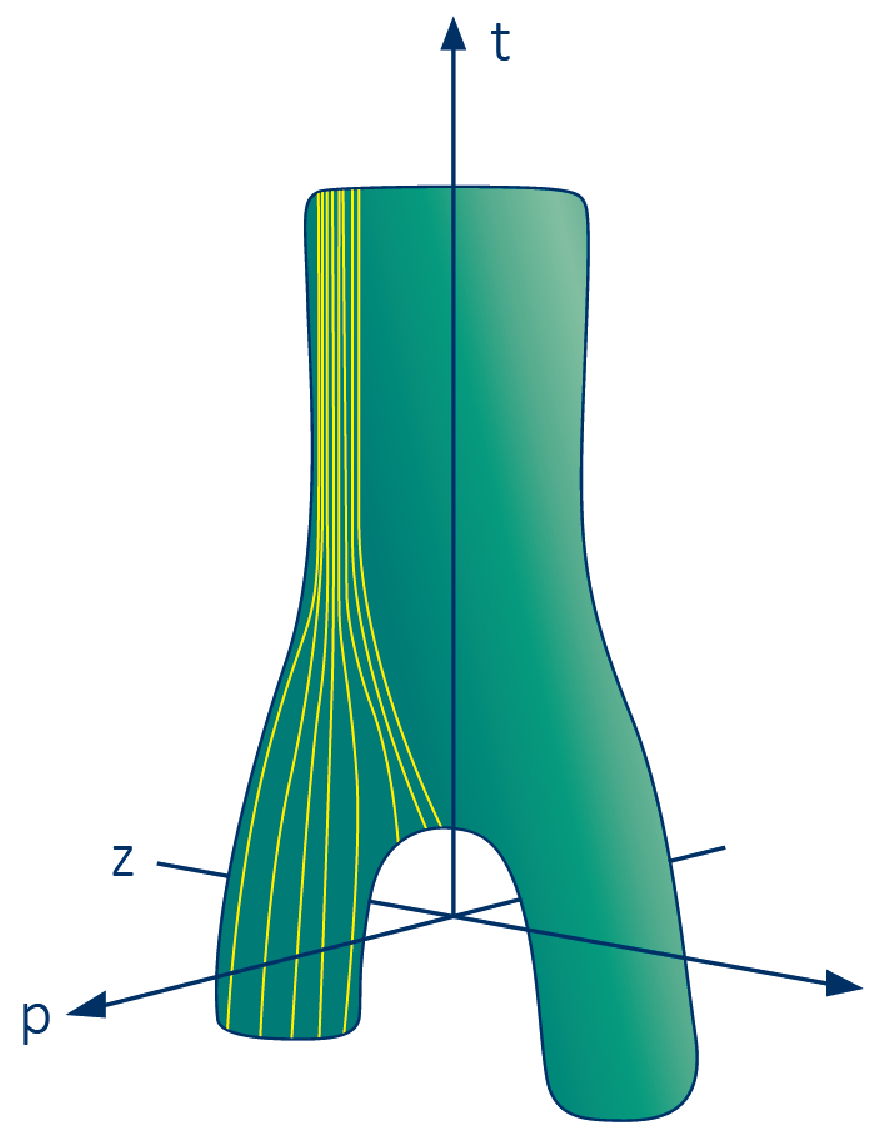
▲圖三：綠色管狀圖形顯示雙黑洞融合的過程，朝上為時間方向，黃線是剛好緊臨事件視界的臨界類光曲線，標示著黑洞的邊界。

 

近期重大突破

21 世紀後有了重大突破。ADM 的變型：BSSN 公式（四位美國與日本科學家的冠名）的出現使的穩定性大增，長時間的雙黑洞或中子星模擬成為可能因此可以計算較遠處、以光速傳遞的重力波波型。2003 年布魯曼模擬出旋進碰撞的最後階段，即「最小不穩定軌道」後的那一瞬間，歷時近 150 M。有趣的是，這時雙中子星碰撞早已成功了，這可能是因為它不牽涉到奇異點處理，即使它乍看之下較困難，需要一併討論重力與複雜的流體。

而在 2004 年左右，也是多核心微處理器逐漸流行的時代。由於處理器的能耗正比於頻率、或是電壓的平方。因此，在相同電晶體的數量下，比起製作一個較大且工作頻率較高的處理器晶片，還不如以較多、頻率相同但較小的晶片，可大幅減少能耗。不過代價是，程式設計師必須考量多核心程式設計，以充分發揮多核心的平行計算能力。此時，最快的超級電腦計算力為 10 TFLOPS（=10¹³ FLOPS）數量級。

2005 年可說是雙黑洞碰撞模擬的元年，人們終於可以計算出黑洞從旋進、碰撞融合、到鈴震並逐漸靜默成單一黑洞的整段波形。這個突破帶領廣義相對論到另一個階段，可進行各種雙黑洞系統參數的數值實驗。分別是由加州理工學院的比勒陀利烏斯（Frans Pretorius），以及以貝克（John Baker）為首的美國太空總署重力與天文物理團隊，與坎帕內利（Manuela Campanelli）為首的德州大學團隊分別獨立完成。令人驚訝的是，後兩者的成功與上世紀末的 BSSN 方法幾乎沒有差別：過去為了避開奇異點（即初始資料的穿刺點），刻意選用特定座標，使黑洞固定在座標上，動的只是座標扭曲程度。一旦把此限制拿掉，座標反而不再扭曲的太厲害，原本擔心的奇異點問題也沒有發生。事後看來，這是因為黑洞的特性就是吸收所有物質、能量、甚至在數值上也包括座標本身，因此，縱然奇異點附近的數值行為讓人不安，但其實並不會對事件視界外有太多影響。

目前，人們可做到融合前多達數十圈的黑洞運行，整個過程估計約損失 5% 質量變成重力波輻射。另一方面，來自於軌道角動量的黑洞自旋約可達最大值的 0.69，因此自然界中若存在接近最大自旋的黑洞，其生成機制也是有趣的問題。即使在目前的超級電腦下，這些模擬也需花上 4、5 天以上。

 

龐大資料處理

有別於上述個別超級電腦或叢集電腦的計算，90 年代興起的格網計算，也讓人們思考是否可用於數值相對論模擬、與結果的視覺化。格網是早在 60 年代初所發想的一種計算模式，希望結合異地、異質資源，最終目的讓使用計算儲存資源有如用水電一般的方便自然，隨取即用。技術上，每一個參與個格網的資源中心、無論是超級電腦還是小型的叢集系統，僅需要安裝特定格網中介軟體，提供抽象層將所有資源虛擬成一個大的資源池。2000 年左右，基於已逐漸成熟的全球網際網路，為了要處理大強子對撞機的全球格網逐漸成形，歐美等地的格網組織紛紛成立，並串聯成全球尺度的科學計算設施。而各國的研究與教育網路（National research and education network, NREN）也陸續而生，作為格網計算的基礎設施網路，也作為一般商業網路的先導測試平台。

這種模式相當適合所謂的傻瓜平行（embarrassingly parallel），即彼此工作是獨立的，沒有相依性，因此網路的延遲並不會拖慢整體計算。但數值相對論適合這類架構嗎？當時人們預想的場景是：一旦重力波觀測器偵測到微弱訊號，需盡快計算可能對應的波形，以作為資料分析的波形模板。原本需要數天或數周的大型模擬，所需硬碟空間甚至可超過單一計算中心的容量，但藉由格網的分散式平行計算，初始條件可能先在德國萊布尼茲超級電腦中心產生，再搬到美國聖地牙哥中心進行模擬；一段時間後，也許再遷移到伊利諾大學的超級電腦應用中心（NCSA），因為後者有較多閒置主機，或是前者因緊急需求暫時收回結點。世界各地的科學家，也可遠端觀察模擬結果並作後續分析。

自從 1993 年後，上述流程數次在美國超級電腦年會上展示，以洲際格網計算進行互動式雙黑洞或雙中子星碰撞模擬，這些研究也是現代格網中介軟體的發展前身。

以現在的眼光來看，這麼做似乎有點累贅。因為對簡單的雙黑洞系統，已有不少解析、半解析波形，例如等效單體模型等，並不總需從頭模擬；另一方面，半導體進展神速，微處理器效能與儲存容量自 80 年代起持續以指數成長，反到是網路頻寬增加與延遲速度降低的程度沒那麼快，成為洲際格網平行計算的瓶頸。因此，格網還是較實用於大型科學實驗的分散式資料處理，如目前最成熟的全球 LHC 計算格網，以及其他百餘個大小不一的應用。數值相對論這類傳統的高速平行計算，彼此間耦合較前者密切，還是較仰賴單一的叢集系統。

對於日益複雜龐大的科學計算、或實驗資料處理，格網計算仍是個進化中、且正在運行的科研基礎設施。不過，本來的資源隨取即用目標，反倒逐漸由市場導向的商業雲端服務逐漸實現，成為日常生活中一部分。科學格網的規模也早已不如 Facebook、Google、Amazon  等大規模資料中心，但都還在大型計畫中扮演要角：例如 LIGO 的重力波分析就是基於 5 萬多個計算核心組成的格網環境。相對於格網計算，數值相對論模擬屬於傳統的高速平行計算，耦合較密切，每台計算結點需頻繁交換資料，因此低延遲高頻寬的內部網路極為關鍵，單一的超級電腦還是較具優勢。

本文試圖呈現早期黑洞模擬與計算科學並行的發展歷程，希望讓讀者感受到理論、演算法與各種計算設施在基礎研究中相同的重要性。雙中子星的重力波事件、與後續一系列的電磁波餘暉，都讓重力波研究與應用的前景毫無疑問地愈來愈樂觀。數值相對論模擬也早已往更複雜的場景推進，解析細微瞬間的動力學演化，探索重力、電磁力、以及高溫與高壓極端物質狀態的微觀過程交互作用。這些除了需要恰當的物理導引，計算技術上的實現與執行力也是少不的。

 

註一：速度的成長主要來自於三個進展：半導體製程（即摩爾定律，指積體電路上單位面積的電晶體數量每兩年成倍增長。由於電晶體的距離靠近，意謂著在相同的工作頻率下，整體速度增加約 40％），微處理器架構（Pollack 準則，是另一個半導體經驗公式，指微處理器性能正比於電晶體數量的開根號），與平行處理的跨節點網路架構。

註二：請參見 TOP500 的效能演化趨勢圖：goo.gl/EAQHNt。

註三：這裡看似為質量的 M，實際上是廣義相對論所慣用「幾何單位制」的時間單位，對應到公制的 MG/c3 秒。因此，一個太陽質量約 5μs。光橫越黑洞的特徵時間約為 4 M，黑洞準正則震盪特徵週期約為 17 M。幾何單位制下的 M 也可代表 MG/c² 公尺，一個太陽質量約 1.5 公里。

 

延伸閱讀

1. Ulrich Sperhake, The numerical relativity breakthrough for binary black holes, arXiv:1411.3997.

2. Luis Lehner, Numerical Relativity: A review, arXiv:gr-qc/0106072.

 

⇠上一篇：太陽系旁有黑洞？第九行星之謎

細胞治療的未來：下一篇⇢

本文轉載、修改自《科學月刊》2018 年 2 月