魏澤人/任教於國立東華大學,創立花蓮——py社群及實做數學粉專。
|
在人工智慧(artificial intelligence, AI)的風潮下,數學科普、教育或者甚至數學本身,微妙地陷入一個尷尬的處境;或者應該說,陷入兩個尷尬處境。 |
我們曾學過的數學,究竟對人生有什麼幫助?
第一個尷尬點是,數學的實用性變得十分明顯,明顯到令人尷尬。學數學的人,常會聽到人問:「學數學有什麼用?」、「我高中數學都忘光了,還不是活得好好的?」、「工作上好像完全沒用到。」、「我寫程式這麼久了,也沒用到什麼數學。」
當然,內行人都知道數學在科學、技術、工程中,應用十分廣泛。特別在網路時代,網路加密、電腦運算、影像壓縮,甚至網頁和應用程式的自動排版都得用到數學。即使連照片編修這種屬於藝術文化的活動,其中的圖層操作就包含了向量概念,調色盤會看到 16 進位及顏色轉換的線性變換,更不用說伽馬校正、貝茲曲線、高斯濾鏡、邊界加強、內容感知拉長、內容感知填滿等功能,處處都是微積分與線性變換,最後如果要輸出 JPEG,也少不了傅立葉轉換和資訊熵。
生活中沒有數學嗎?只要知道看哪裡,你根本沒辦法不看到,到處都是密密麻麻的數學。高中生所學習的 log 與三角函數絕對不是徒勞無功,若沒有三角函數及 log 的幫忙,我們無法像現在這樣隨時都能輕鬆地拿出手機拍照,就算不懂數學,數學也能默默發揮功用。然而,若看不到數學,人們可能會活在一個非常無聊的世界,一個很多東西都看不到的世界、失去顏色跟細節的世界。
寶寶知道數學有用,但寶寶很難說清楚。
「那些聽不見音樂的,認為那些跳舞的人都瘋了的」,在哈利波特的魔法世界中,看不見魔法的人覺得魔法師都是怪胎和瘋子。我們也許像查拉圖斯特拉一樣願意相信一位會跳舞的神,但對於還不能聽到音樂的人來說,我們光在那跳來跳出、跟他說音樂有多好聽,只會被當成瘋子,就像巫師世界不會對看不到魔法的一般群眾推廣魔法的好處一樣。當然,身為數學專業人員,在數學科普推廣方面,情況也不是那麼一籌莫展。我們嘗試了各式各樣的方法與理論,來讓一般大眾了解數學的好處,如邏輯訓練、數學遊戲等等。讀到這裡,應該也大致了解數學專業人員在社交場合及招生推廣方面的一些困境及努力,常常需要像是「無用之用方為大用」這些論點及觀點來循循善誘,說明數學「隱藏」的好處。
在這個時代裡,數學能為何所用?
在深度學習及人工智慧成為顯學的今日,情形已經有所不同;原來隱藏的魔法世界就像突然曝光似的,數學的用途變得顯而易見。
電腦工程師們重新拿起統計、微積分及線性代數課本,想要了解現代的人工智慧在玩什麼把戲。現代人工智慧的領軍人物之一勒丘恩(Yann LeCun)說「人工智慧就是數學(artificial intelligence is all about math)」,他給想從深入人工智慧領域大學生的建議是:「如果在『iOS 程式設計』及『量子力學』中要選一門課來修的話,選量子力學,且一定要選修微積分一、微積分二、微積分三……、線性代數、機率與統計,和盡可能的多選物理課程。即便如此,最重要的還是要會寫程式。」
大眾能認同數學的實用性和好處,對數學推廣來說,自然是好事;問題是,辦到這件事情的人,不是數學家和數學老師。除了情況有些困窘外,之前大言不慚「無用之用是為大用」之類的講法,相形之下更加空虛寂寞,而數學遊戲、魔術等等親民的方式,相形之下也變得太過可愛,甚至有點多餘。撇開面子層面,更實際問題是,大部分數學老師不見得清楚人工智慧的進展以及數學在其中扮演的角色然而其實有很多地方能跟數學課程連結。另外一個熱門的技術──「區塊鏈(block chain)」也有一堆數學課程內容能夠連結,但並非多半數學教師不熟悉。不過在此我們先把重點放在人工智慧這塊。人工智慧、機器學習、深度學習裡,究竟用到了什麼數學呢?

▲圖二:尼采:「我只願意相信一位會跳舞的神。」圖片來源/Wikipedia
極值問題與梯度下降法
在深度學習相關的數學中,最先被提到的往往是「梯度下降法(gradient descent)」。梯度,即 gradient,簡單來說就是多變數函數的微分,而梯度下降法廣泛用來處理「極值問題」。在深度學習、機器學習中常會設計一個損失函數(loss function),用來評估機器有多接近我們的理想目標。越接近理想的行為,比方說文字與圖片辨識得越準確、下棋下得越好、翻譯得越正確,那損失函數的值就會越小,如此一來只要找到適當的參數,讓損失函數盡量小,那機器就能執行我們希望的行為。
這個損失函數一定都是數學上能計算的函數,而這就是數學上標準的極值問題,有很多方法來處理。其實不只是機器學習與人工智慧,許多的科學、工程技術、甚至日常生活問題,都能以極值問題的形式出現。舉例來說,當你快樂地計畫著出門旅行,就會碰到好幾個極值問題:在你收拾行李時,想在有限的包包裡塞入最多的物品,就是一個有名的組合極值問題──「背包問題(Knapsack problem)」;你想要用最短的路徑、時間來參觀所有景點,又會碰上另外一個有名的組合極值問題──「旅行推銷員問題(Traveling salesman problem)」。兩個極值問題都以「困難」聞名,屬於 NP 完全問題,在某種理論意義上要完整解決這些問題,至少跟破解 RSA 密碼一樣難(一般相信是比破解 RSA 更難)。
不過這兩個問題都是「離散」的極值問題,好在深度學習中,我們要處理的損失函數通常是「連續」的。而微積分就是處理「連續」問題的利器。在談到數學有多可怕時,「微積分」常常被拿來扮演虎姑婆或者大野狼這種嚇人的角色。但就像創立現代電腦與博奕論的數學家馮紐曼(John von Neumann)說的:「如果人們不相信數學很簡單,那只是因為他們沒有發現生活有多複雜。」,真要比較的話,出門旅行要比微積分複雜而困難得多,因為「連續」是一種規律,而有規律才可能讓問題變簡單。

▲圖一:馮紐曼曾說,如果人們不相信數學很簡單,那只是因為他們沒有發現生活有多複雜。圖片來源/Wikipedia
連續極值問題中,梯度就是這樣被利用的。在數學上,我們知道梯度是函數值上升最快的方向,而反梯度方向則是下降最快的方向,所以我們只要把「損失函數」對我們想調整的「參數」去微分得到梯度,然後就知道要往哪個方向去調整參數、進而讓損失函數有效地降低。這樣簡單到有點天真的想法,真的有效嗎?在某些假設下,還真的能讓我們找到最好的參數,而深度學習中的損失函數,其實常常不合乎這些假設,就像馮紐曼說的,真實生活比數學複雜,既然沒什麼辦法可言,就閉著眼睛拿梯度下降法來用看看吧!還好,常常也能得到夠好的結果。在這個基礎上,將原始梯度下降法做了一些改良,調整每次下坡的幅度,就是現今深度學習大量使用的方式。此外,除了梯度下降法這類的一次微分方法外,利用二次微分的牛頓法及用近似二次微分的擬牛頓法也常常用來解決極值問題。在深度學習中,像是圖片畫風轉移,有時也會利用這些方法。

▲圖三:勒丘恩:「人工智慧完全是數學。」圖片來源/Wikipedia
反向傳播算法、合成函數及連鎖法則
梯度下降法的確能有效,但前提是要能將損失函數對參數微分,有時函數比較簡單一點,像是線性迴歸或邏輯迴歸(logistic regression),微分起來還算簡單,但深度學習用的類神經網路(artificial neural network)就複雜多了。當簡單的模型不足以應付複雜任務時,我們就需要更複雜的網路。數學上處理複雜事物的一種標準作法,就是分而擊之:先將大問題分成幾個小問題,然後各個擊破。比方說數學歸納法就是典型的例子:有無窮多個式子要證明?不要緊,找出規律、一次只處理一個情況即可;線性代數中的基底也是,將複雜的情形分解成有線情形的線性組合;而合成函數是另外一個例子,用簡單的函數組合出複雜的函數。所以在微積分中,我們只要知道基本函數的微分即可。更複雜的函數,只要看成是基本函數的合成函數就行了,藉由連鎖法則(Chain rule),就能把合成函數的微分計算出來,而神經網路也是這樣的概念。邏輯迴歸或者線性迴歸太簡單、不夠用?把這些簡單的函數一層一層合成在一起就變複雜了。而微分呢?交給連鎖法則就行了。看起來問題解決了。但不是都說深度學習神經網路要靠反向傳播算法(Back Propagation)嗎?怎麼都沒有看到呢?
反向傳播算法基本上就是連鎖法則。啊,又是一個裝潮的時下用語(buzzword)?
▲圖五:連鎖法則示意圖。
這樣講會碰到一些自動微分技術專家的逆鱗。其實數學上的公式本身是一個敘述,闡明一項數學上的事實,並不代表計算的方式與過程,真的要計算時,往往會有很多不同的路徑可以選擇。像是當我們想計算 56×123 時,並不一定要照定義真的把 123 個 56 加在一起;要計算 216 時,也不一定真的要照字面上真的把 16 個 2 乘在一起。真要計算連鎖法則時,也是有很多不同的方法和考量,包括數值計算上的考量,這裡面也有不少學問的,然而對於踩在數學科普推廣位置上的人,還是要處變不驚地說:「反向傳播算法就是連鎖法則」。
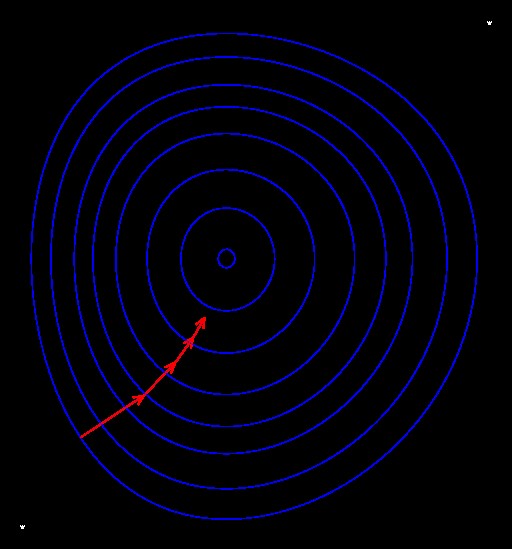
▲圖四:梯度下降法示意圖。圖片來源/Wikipedia
線性代數
只要有簡單的函數,就能組成複雜的神經網路。但什麼是簡單的?人類最直覺簡單的,就是「線性組合」,這樣講可能很多人不服氣,因為線性組合的概念,非常穩定及持續地困擾著數學系的學生,然而只要路上繞個一圈,就會發現我們一天到晚都在用到線性組合的概念,像是:去市場買東西時,你會買「1 打蛋、7 顆蘋果、1 袋鹽、1 包米」;醫師開立處方「每餐飯後 2 粒黃藥丸、1 粒白藥丸、5 c.c. 透明藥水,發燒時加上半顆紅色藥丸」;炒菜時「半匙鹽、1 匙油、3 顆蒜頭」;訂位「6 張大人、4 張學生票、3 張老人票」;訂購衣服「5 件 S、3 件 M、2 件 L、2 件 XL」;吃早餐「2 個培根蛋、1 個原味蛋餅、1 個蘿蔔糕、3 杯紅茶」等。
發現規律了嗎?數學上的線性空間,依照定義簡而言之,就是一些能以加法及純量乘法的「東西」所形成的空間,純量乘法聽起來高深,其實說的就是「n 個 XX」這件事情。n 是一個數字,稱為純量,而 XX 就被當成向量。 但加法又是怎麼一回事呢?1 顆蘋果跟 3 顆橘子能加在一起嗎?當然可以,反正最後都要一起算錢,而算錢的操作基本上就是一個線性變換,從多維度的物品線性空間映射到一維度金錢空間。當然這個模型並不是很精確,因為買東西有時會有買一送一之類的優惠。就說了,現實生活比數學要複雜得多了,但線性模型仍然相當實用。
深度學習神經網路中的每一層,使用的就是簡單的線性變換。為了效率,常使用捲積這類速度較快的線性變換。然後把許多線性變換疊一起,當然為了使這些線性變換不會垮掉,中間會放一些非線性函數,但主要學習的參數還是這些線性變換的矩陣。

▲圖六:馬克佐伯格:「凡是我們不了解的,就稱為 AI。一旦我們了解了,就稱之為數學。」
圖片來源/flickr-Presidencia de la República Mexicana, https://flic.kr/p/p3PE7h
魔法與數學
另外一個最直覺的方式,就是機率與統計的模型。不過我們先談談另外一個數學教育及推廣的尷尬點:深度學習缺乏解釋力。臉書創始人佐伯格(Mark Elliot Zuckerberg)在談到數學與 AI 的分野時曾說:「AI 有點像是魔法,凡是我們不了解的,就稱為 AI;一旦我們了解了,就稱之為數學。一些 30 年前被認為是 AI 的東西 ……現在看起來只是數學。」目前深度學習的人工智慧,最被質疑的一個部份,就是「可解釋性」,因為在很大程度上,訓練出來的神經網路,就像一個黑箱一樣,我們雖然清楚所有參數的值、也了解中間運算的過程,但是當一個人工智慧拒絕了某個貸款申請,判定某個人要開刀,我們很難對申請者或者病患說明是什麼原因拒絕貸款申請、或者需要開刀。當然我們可以把人工智慧的貸款分數對申請者的資料去微分,然後告訴申請者「梯度」,但我很懷疑申請者是否會接受這個理由。
的確,人工智慧彰顯了數學的威力與實用性,但在某種意義上,與數學的本質背道而馳。數學在本質上,就是人類理解思考背後邏輯的方式,嚴格數學證明的每一步驟,都要給出理由。10 年前,在深度學習崛起前。許多人工智慧是以統計方法完成的,像是用貝氏方法過濾垃圾信、統計機器翻譯、高斯混何模型等。作為資料分析的重要方法,統計有著大量的理論基礎,有許多能提供解釋的方法,在各學門研究中被廣泛運用。深度學習的理論及技術中,不少地方也需要有機率及統計的概念;整體來說,解釋力是深度學習的一個重要問題。有不少研究在設法解決這個問題。現況是在很多應用中,深度學習提供了較高的準確度,但也缺乏了解釋力。準確度高的黑箱模型,和準確度較低的白箱模型,你會選哪個?這是目前應用上需要取捨的抉擇。
數學長期以來,作為科學研究的主要支持者,同時精確地描述科學理論模型以及預測現象。數學文化上也支持理性及邏輯。用理性的方式建立科學模型,然後預測自然現象,這中間根本理所當然吧?但由於深度學習的出現,嘗到了模型的「解釋力」及「預測力」產生矛盾的滋味,有點像一個以高科技生產零件而自豪的工廠,現在卻因為這些零件能組合出魔法道具而出名。

▲圖七:王爾德:「真相很少單純,也從不簡單。」圖片來源/wikipedia
真相、幻覺與未來
也許會如同佐伯格說的,30 年之後,當我們對深度學習更加了解之後,這些原本的黑箱魔法也變成了數學,但也有可能如王爾德(Oscar Wilde)的名言:「真相很少單純,也從不簡單」,或許宇宙的法則、人類的行為、社會的現象,本來就不依循簡單的模型和數學式子分析,事物的結果都是眾多因素累積疊加的結果。考試沒考好從來都不能簡單歸因為「不夠努力」、「沒睡飽」這樣簡單的因素;一個失敗的政策、體重變重,都是複雜因素綜合的結果。「該負責的是誰?」、「 運動還是飲食比較重要?」根本就不是正確的問題,原因、理由什麼的,也許只是人類意識製造出來,讓自己比較舒服的幻境。
數學從數千年前,就開始為了人類的理性而服務,從畢達哥拉斯、微積分的發展、集合論的發展,經過多次的自我革命與挑戰。很遺憾的,我們無法躬逢其盛,只能從歷史緬懷,而人工智慧的衝擊,是否是數學新一波典範轉移(paradigm shifting)的契機呢?
我完全不知道,但感覺一定會很有趣。
延伸閱讀
歐柏昇,〈涂林機到人工智慧,誰讓電腦強大?是數學!〉,研之有物,https://goo.gl/NkkneV。
函數、神經網路與深度學習:下一篇⇢





















